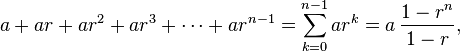EDIT: I’ve just been informed that the additional Red Fury attacks do not benefit from Red Fury so this is no longer accurate. I’ll leave it up as it’s still an interesting exercise For now though, I’m off to call Ben a filthy cheat.
It’s been a little while since I’ve done a Math-hammer post, so I’d thought I’d bust one out.
I’ve recently started a Battlefields: Lustria campaign with my friend, Ben, where I’m playing Lizardmen as the invaders and he’s playing Vampire Counts as the custodians. We decided to try and keep the same list for the whole campaign as neither of us had tried out these new campaigns and didn’t want to constantly try to out metagame each other. We also picked 1,600 points because in our experience, that’s a good size to keep games around about 2 hours on Universal Battle and to not have too many things going on that we forget lots.
I might talk more about the campaign in detail once we’ve finished it but for this post, suffice it to say, I lost the first scenario. His Vampire Lord was terrifying. He was using Quickblood to give it Always Strikes First, The Ogre Blade to make him Strength 7 and Red Fury meaning that for each wound dealt, he would be granted another attack. I believe the term bandied around the internet Warhammer scene is “Blender Lord”.
Against most of my things, he was hitting on 3+ with a reroll due to Always Strikes First and then wounding on 2+, completely negating my save. After breaking a Skink Cohort by killing all three Kroxigors and a handful of Skinks and then destroying 20 Temple Guard to a man, my army was devastated and I started to wonder if I was getting unlucky or the Vampire was just really, really strong. Today at work we were discussing it and it seems in the first combat, it was about right and the second one, I was relatively unlucky.
Let’s look at some of those expected values. To start with, we’ll consider the simple example: hitting on 3+ with the reroll, wounding on 2+. As a quick aside, when considering probabilities, it’s easy to think of “and” as multiplication and “or” as addition. From there, the chance of a wound for any single attack is the chance that you hit AND wound OR the chance that you miss AND hit the reroll AND wound. I.e.:
With his 5 attacks, we get to:
wounds after the initial attacks. The trick here is the Red Fury means he attacks that many times again which also wound on the same probability. So we have total number of wounds dealt as:
Then those additional 2.7 wounds also cause more hits so we’re looking at:
The pattern here is pretty easy to spot. It’s a geometric series {a,ar,ar2,ar3,…} where a = 5×(20/27) and r = (20/27). Luckily there’s a simple formula to work out the sum of a series like this.
To see if this series converges, let’s consider if n continued to infinity. As 0 < r < 1, we can see that rn approaches 0. This means our formula becomes a/(1-r) and a quick substitution of a and r shows that the total expected number of wounds in this scenario is 100/7 ≃ 14.2. Ouch!
In order to work out how likely you are to blend a unit, all you need to know is how likely you are to cause an unsaved wound and how many attacks you’ll have. Then you set a equal to the number of attacks times the likelihood of an unsaved wound and r equal to the likelihood of an unsaved wound, calculate a/(1-r) and you have it!
I’ve built a little tool to calculate the likelihood given a few different parameters. You’ll find it in the sidebar. Let me know if it produces any odd results, the testing I’ve done is minimal.